7 Direction tuning

This type of plot is so fundamental to the examination of LM and nBOR, it deserves a chapter unto itself. The majority of the information going into polar tuning plots is the same as those in previous chapters. Unlike raster and mean spike rate plots, however, direction tuning plots require deliberate choices from the investigator to delineate a “baseline” spike rate to be distinguished from the spike rate during the stimulus of interest (in our case, global motion patterns). The conditions that define the baseline and motion epochs require explicit definitions form the investigator.

Seeing the mean spike rate plot from the previous chapter will help give context to some of these decisions [INSERT IMAGE HERE]. Importantly, at the onset of the blank and the stationary phases, it is common to observe an initial transient response – a sharp increase in the spike rate of the neuron – followed by a return to a steady state.

For our purposes, the baseline will be defined as the steady state response during the stationary phase of the stimulus. We will collect this steady state response rate across all stimulus conditions (i.e., varying combos of speed and direction), and will simply average all of those response rates to attain our baseline rate (and its SEM). Please note that it is up to the investigator to determine if this definition is appropriate, especially if other stimulus presentations are being used.

For the “motion epoch”, I will use a few different definitions. Some of these conventions are informed by previous work (e.g., Smyth et al. 2022), whereas others are just based on a rough approximation of what may be appropriate for these data. The definitions of the motion epochs will be:

1. The entire 3-sec motion epoch
2. The “initial transient” phase: 40-200ms after the onset of motion (as used in Smyth et al. 2022)
3. The “steady state” phase: 1500-3000ms after the onset of motion, a.k.a., the second half of the motion stimulus (as used in Smyth et al. 2022)
4. The first 500 ms of the motion phase. This is an arbitrary definition for demonstrative purposes only, but somewhat informed by observing the patterns in the mean spike rate plot

As we construct polar plots, two additional aspects will be included in the plots:

1. The “preferred direction” of the neuron, as defined by the vector sum method [insert citation]. This will be shown as a single grey line in the plot that indicates the preferred direction. Bear in mind that this value may not always be meaningful, particularly in cases of multi-modal responses.
2. The Sensitivity Index (SI) of the neuron, as defined by citation. This metric calculates the narrowness of tuning. An SI of 1 indicates strong response to a single direction whereas 0 indicates similar response across all investigated directions.

7.1 Data import and baseline rate measurement

We will use the 10-ms binned data for these examples. We’ll read in the file and then extract the baseline rate as defined above. The code will be written such that it can batch-process more than one file if desired.

bin10_data <- NULL
polar_directions <- NULL
baseline_summary_df <- NULL
for (i in 1:length(bin10_filelist)) {
  ## Read in the data
  bin10_data[[i]] <-
    read_csv(bin10_filelist[i], show_col_types = FALSE) %>%
    as_tibble()

  ## get unique speeds
  sorted_speeds <-
    bin10_data[[i]]$Speed %>% unique %>% sort(decreasing = TRUE)

  ## Again, we will set Speed as an ordered factor to help control plotting
  ## later on
  bin10_data[[i]] <-
    bin10_data[[i]] %>%
    mutate(
      Speed = factor(Speed,
                     levels = sorted_speeds))

  ## Determine unique directions
  polar_directions[[i]] <-
    bin10_data[[i]]$Direction %>%
    unique()

  ## Extract all rows corresponding to our desired baseline epoch
  baseline_df <-
    bin10_data[[i]] %>%
    filter(Time_stand >= Blank_end + 0.5) %>% ## 0.5 sec after blank end
    filter(Time_stand <= Static_end - 0.05)   ## 0.05 sec before static end

  ## Compute the mean baseline
  global_base <- mean(baseline_df$Spike_rate)
  ## Compute the SE
  global_base_se <-
    sd(baseline_df$Spike_rate) / sqrt(length(baseline_df$Spike_rate)
    )

  ## Construct a summary data frame
  baseline_summary_df[[i]] <-
    baseline_df %>%
    group_by(Speed) %>%
    summarize(
      speed_specific_baseline = mean(Spike_rate),
      speed_specific_baseline_se = sd(Spike_rate)/sqrt(length(Spike_rate)),
      global_baseline = global_base,
      global_baseline_se = global_base_se
    )

  ## This tibble contains speed-specific baselines (and SE) along with the
  ## global mean baseline (and SE)
  baseline_summary_df[[i]]
}

7.2 Using the full 3-sec motion epoch

This will be referred to as the “naive” approach in the code below

## global baseline values, full 3-sec motion period
bin10_polar_naive <- NULL
for (i in 1:length(bin10_filelist)) {
  naive_df  <-
    bin10_data[[i]]  %>%
    filter(Time_stand > Static_end) %>%
    group_by(Speed, Direction, Replicate) %>%
    summarize(
      mean_spike_rate = mean(Spike_rate)
    )
  naive_360 <-
    naive_df %>%
    filter(Direction == 0) %>%
    transmute(
      Speed = Speed,
      Direction = 360,
      Replicate = Replicate,
      mean_spike_rate = mean_spike_rate)
  naive_vecsum_df <-
    naive_df %>%
    ungroup() %>%
    drop_na(mean_spike_rate) %>%
    group_split(Speed) %>%
    map(group_by, Direction) %>%
    ## NOTE: FOLLOWING THE JNP AND CB PAPERS, WE ARE SUBTRACTING BASELINE HERE AND
    ## THEN IF ANY AVERAGED FIRING RATES ARE NEGATIVE, THEY ARE SHIFTED SO THE
    ## LOWEST ONE IS ZERO. THE GENERATED PLOTS STILL SHOW NON-BASELINE-SUBTRACTED
    ## FIRING RATES (AND BASELINE AS A RED RING), BUT COMPUTATION OF VECTOR SUM
    ## AND SI HAVE BEEN BASELINE SUBTRACTED (AND THE ENTIRE CURVE IS SHIFTED
    ## UPWARDS IF ANY PART IS NEGATIVE)
    map(
      summarize,
      mean_spike_rate = mean(mean_spike_rate) - unique(baseline_summary_df[[i]]$global_baseline),
      Speed = first(Speed)
    ) %>%
    map(mutate,
        mean_spike_rate =
          case_when(
            min(mean_spike_rate) < 0 ~ mean_spike_rate + abs(min(mean_spike_rate)),
            TRUE ~ mean_spike_rate
          )) %>%
    map(
      transmute,
      x = cos(Direction * pi / 180) * mean_spike_rate,
      y = sin(Direction * pi / 180) * mean_spike_rate,
      Speed = first(Speed)
    ) %>%
    map(summarise,
        x = mean(x),
        y = mean(y),
        Speed = first(Speed)) %>%
    map(transmute,
        vector_sum = (atan2(y, x) * 180 / pi) %% 360,
        Speed = first(Speed)) %>%
    bind_rows()
  naive_si_df <-
    naive_df %>%
    ungroup() %>%
    drop_na(mean_spike_rate) %>%
    group_split(Speed) %>%
    map(group_by, Direction) %>%
    map(
      summarize,
      mean_spike_rate = mean(mean_spike_rate) - unique(baseline_summary_df[[i]]$global_baseline),
      Speed = first(Speed)
    ) %>%
    map(mutate,
        mean_spike_rate =
          case_when(
            min(mean_spike_rate) < 0 ~ mean_spike_rate + abs(min(mean_spike_rate)),
            TRUE ~ mean_spike_rate
          )) %>%
    map(
      transmute,
      a = (sin(Direction * pi / 180) * mean_spike_rate),
      b = (cos(Direction * pi / 180) * mean_spike_rate),
      c = mean(mean_spike_rate),
      Speed = first(Speed)
    ) %>%
    map(
      summarise,
      a = mean(a),
      b = mean(b),
      c = mean(c),
      Speed = first(Speed)
    ) %>%
    map(transmute,
        si = sqrt(a ^ 2 + b ^ 2) / c,
        Speed = first(Speed)) %>%
    bind_rows()

  naive_data <-
    naive_df %>%
    bind_rows(naive_360) %>%
    left_join(naive_vecsum_df, by = "Speed") %>%
    left_join(naive_si_df, by = "Speed") %>%
    drop_na(mean_spike_rate)
  naive_max_y <- max(naive_data$mean_spike_rate)

  bin10_polar_naive[[i]] <-
    naive_data %>%
    left_join(baseline_summary_df[[i]], by = "Speed") %>%
    ggplot(aes(x = Direction, y = mean_spike_rate)) +
    geom_ribbon(aes(
      x = Direction,
      ymin = global_baseline - global_baseline_se,
      ymax = global_baseline + global_baseline_se
    ),
    fill = "darkgoldenrod1") +
    stat_smooth(method = "glm",
                formula = y ~ ns(x, length(polar_directions[[i]])),
                linewidth = 0.3, color = "forestgreen") +
    geom_point(color = "#333132") +
    geom_label(aes(label = round(si, 2) , x = 315, y = naive_max_y * 1.2),
               size = 3) +
    geom_vline(aes(xintercept = vector_sum), colour = "grey30",
               size = 0.75) +
    coord_polar(direction = 1, start = pi / 2) +
    scale_x_continuous(
      breaks = c(0, 90, 180, 270),
      expand = c(0, 0),
      limits = c(0, 360)
    ) +
    scale_y_continuous(
      #trans = "sqrt",
      limits = c(0, naive_max_y * 1.2)
    ) +
    facet_grid(cols = vars(Speed)) +
    ggtitle("Full 3-sec motion") +
    ylab("Spike rate (spikes/sec)") +
    theme_minimal()
}

## `summarise()` has grouped output by 'Speed', 'Direction'. You can override
## using the `.groups` argument.

## Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
## ℹ Please use `linewidth` instead.

bin10_polar_naive[[1]]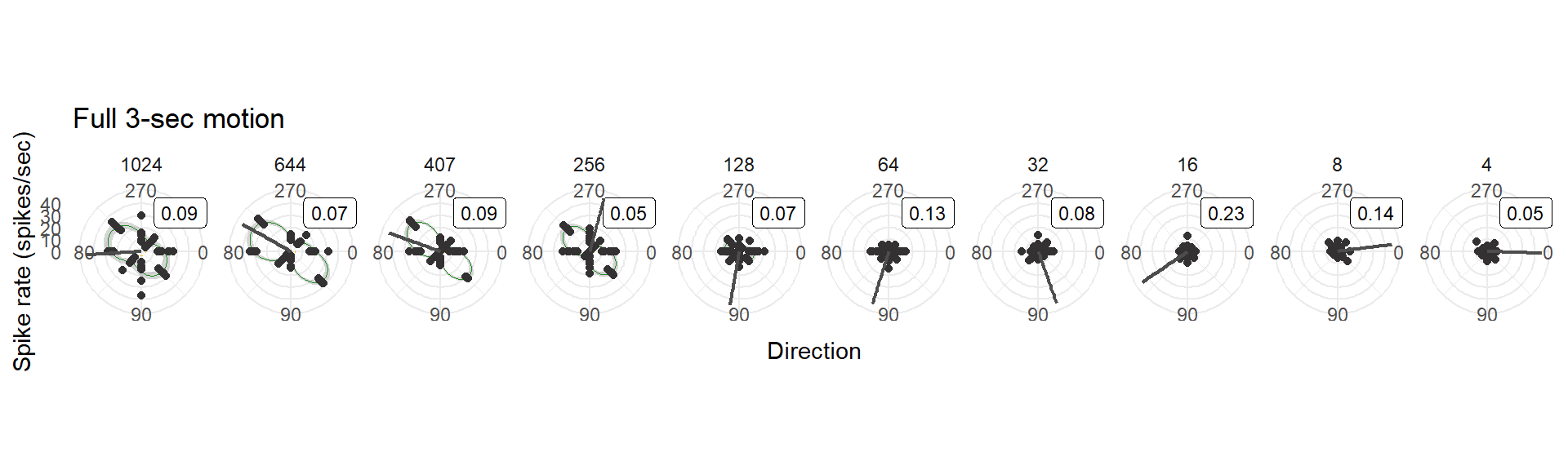

7.3 Using 40-200ms (“initial transient”)

## global baseline values, 40-200 msec motion period
bin10_polar_cbit <- NULL
for (i in 1:length(bin10_filelist)) {
  cbit_df <-
    bin10_data[[i]] %>%
    filter(Time_stand >= Static_end + 0.04) %>%
    filter(Time_stand <= Static_end + 0.2) %>%
    group_by(Speed, Direction, Replicate) %>%
    summarize(
      mean_spike_rate = mean(Spike_rate)
    )
  cbit_360 <-
    cbit_df %>%
    filter(Direction == 0) %>%
    transmute(
      Speed = Speed,
      Direction = 360,
      Replicate = Replicate,
      mean_spike_rate = mean_spike_rate)
  cbit_vecsum_df <-
    cbit_df %>%
    ungroup() %>%
    drop_na(mean_spike_rate) %>%
    group_split(Speed) %>%
    map(group_by, Direction) %>%
    map(summarize,
        mean_spike_rate = mean(mean_spike_rate) - unique(baseline_summary_df[[i]]$global_baseline),
        Speed = first(Speed)) %>%
    map(mutate,
        mean_spike_rate =
          case_when(min(mean_spike_rate) < 0 ~ mean_spike_rate + abs(min(mean_spike_rate)),
                    TRUE ~ mean_spike_rate)) %>%
    map(transmute,
        x = cos(Direction * pi / 180) * mean_spike_rate,
        y = sin(Direction * pi / 180) * mean_spike_rate,
        Speed = first(Speed)
    ) %>%
    map(summarise,
        x = mean(x),
        y = mean(y),
        Speed = first(Speed)) %>%
    map(transmute,
        vector_sum = (atan2(y, x) * 180 / pi) %% 360,
        Speed = first(Speed)
    ) %>%
    bind_rows()
  cbit_si_df <-
    cbit_df %>%
    ungroup() %>%
    drop_na(mean_spike_rate) %>%
    group_split(Speed) %>%
    map(group_by, Direction) %>%
    map(summarize,
        mean_spike_rate = mean(mean_spike_rate) - unique(baseline_summary_df[[i]]$global_baseline),
        Speed = first(Speed)) %>%
    map(mutate,
        mean_spike_rate =
          case_when(min(mean_spike_rate) < 0 ~ mean_spike_rate + abs(min(mean_spike_rate)),
                    TRUE ~ mean_spike_rate)) %>%
    map(transmute,
        a = (sin(Direction * pi / 180) * mean_spike_rate),
        b = (cos(Direction * pi / 180) * mean_spike_rate),
        c = mean(mean_spike_rate),
        Speed = first(Speed)
    ) %>%
    map(summarise,
        a = mean(a),
        b = mean(b),
        c = mean(c),
        Speed = first(Speed)) %>%
    map(transmute,
        si = sqrt(a ^ 2 + b ^ 2) / c,
        Speed = first(Speed)
    ) %>%
    bind_rows()

  cbit_data <-
    cbit_df %>%
    bind_rows(cbit_360) %>%
    left_join(cbit_vecsum_df, by = "Speed") %>%
    left_join(cbit_si_df, by = "Speed") %>%
    drop_na(mean_spike_rate)
  cbit_max_y <- max(cbit_data$mean_spike_rate)

  bin10_polar_cbit[[i]] <-
    cbit_data %>%
    left_join(baseline_summary_df[[i]], by = "Speed") %>%
    ggplot(aes(x = Direction, y = mean_spike_rate)) +
    geom_ribbon(aes(
      x = Direction,
      ymin = global_baseline - global_baseline_se,
      ymax = global_baseline + global_baseline_se
    ),
    fill = "darkgoldenrod1") +
    stat_smooth(method = "glm",
                formula = y ~ ns(x, length(polar_directions[[i]])),
                linewidth = 0.3, color = "forestgreen") +
    geom_point(color = "#333132") +
    geom_label(aes(label = round(si, 2) , x = 315, y = cbit_max_y * 1.2),
               size = 3) +
    geom_vline(aes(xintercept = vector_sum), colour = "grey30",
               size = 0.75) +
    coord_polar(direction = 1, start = pi/2) +
    scale_x_continuous(
      breaks = c(0, 90, 180, 270),
      expand = c(0, 0),
      limits = c(0, 360)
    ) +
    scale_y_continuous(
      #trans = "sqrt",
      limits = c(0, cbit_max_y * 1.2)
    ) +
    facet_grid(cols = vars(Speed)) +
    ggtitle("40-200 ms (initial transient) motion") +
    ylab("Spike rate (spikes/sec)") +
    theme_minimal()
}

## `summarise()` has grouped output by 'Speed', 'Direction'. You can override
## using the `.groups` argument.

bin10_polar_cbit[[1]]

## Warning: Removed 149 rows containing missing values (`geom_smooth()`).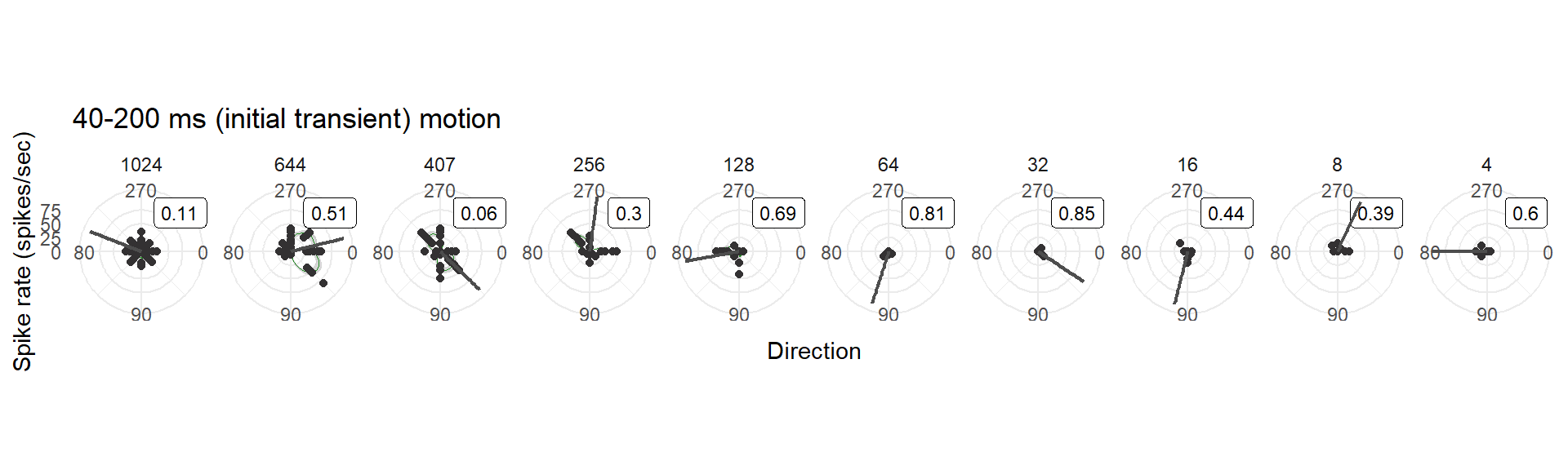

7.4 Using 1500-3000ms (“steady state”)

## global baseline values, second half of motion period
bin10_polar_cbss <- NULL
for (i in 1:length(bin10_filelist)) {
  cbss_df <-
    bin10_data[[i]] %>%
    filter(Time_stand > Static_end + 1.5) %>%
    filter(Time_stand < 4.95) %>%
    group_by(Speed, Direction, Replicate) %>%
    summarize(
      mean_spike_rate = mean(Spike_rate)
    )
  cbss_360 <-
    cbss_df %>%
    filter(Direction == 0) %>%
    transmute(
      Speed = Speed,
      Direction = 360,
      Replicate = Replicate,
      mean_spike_rate = mean_spike_rate)
  cbss_vecsum_df <-
    cbss_df %>%
    ungroup() %>%
    drop_na(mean_spike_rate) %>%
    group_split(Speed) %>%
    map(group_by, Direction) %>%
    map(summarize,
        mean_spike_rate = mean(mean_spike_rate) - unique(baseline_summary_df[[i]]$global_baseline),
        Speed = first(Speed)) %>%
    map(mutate,
        mean_spike_rate =
          case_when(min(mean_spike_rate) < 0 ~ mean_spike_rate + abs(min(mean_spike_rate)),
                    TRUE ~ mean_spike_rate)) %>%
    map(transmute,
        x = cos(Direction * pi / 180) * mean_spike_rate,
        y = sin(Direction * pi / 180) * mean_spike_rate,
        Speed = first(Speed)
    ) %>%
    map(summarise,
        x = mean(x),
        y = mean(y),
        Speed = first(Speed)) %>%
    map(transmute,
        vector_sum = (atan2(y, x) * 180 / pi) %% 360,
        Speed = first(Speed)
    ) %>%
    bind_rows()
  cbss_si_df <-
    cbss_df %>%
    ungroup() %>%
    drop_na(mean_spike_rate) %>%
    group_split(Speed) %>%
    map(group_by, Direction) %>%
    map(summarize,
        mean_spike_rate = mean(mean_spike_rate) - unique(baseline_summary_df[[i]]$global_baseline),
        Speed = first(Speed)) %>%
    map(mutate,
        mean_spike_rate =
          case_when(min(mean_spike_rate) < 0 ~ mean_spike_rate + abs(min(mean_spike_rate)),
                    TRUE ~ mean_spike_rate)) %>%
    map(transmute,
        a = (sin(Direction * pi / 180) * mean_spike_rate),
        b = (cos(Direction * pi / 180) * mean_spike_rate),
        c = mean(mean_spike_rate),
        Speed = first(Speed)
    ) %>%
    map(summarise,
        a = mean(a),
        b = mean(b),
        c = mean(c),
        Speed = first(Speed)) %>%
    map(transmute,
        si = sqrt(a ^ 2 + b ^ 2) / c,
        Speed = first(Speed)
    ) %>%
    bind_rows()

  cbss_data <-
    cbss_df %>%
    bind_rows(cbss_360) %>%
    left_join(cbss_vecsum_df, by = "Speed") %>%
    left_join(cbss_si_df, by = "Speed") %>%
    drop_na(mean_spike_rate)
  cbss_max_y <- max(cbss_data$mean_spike_rate)


  bin10_polar_cbss[[i]] <-
    cbss_data %>%
    left_join(baseline_summary_df[[i]], by = "Speed") %>%
    ggplot(aes(x = Direction, y = mean_spike_rate)) +
    geom_ribbon(aes(
      x = Direction,
      ymin = global_baseline - global_baseline_se,
      ymax = global_baseline + global_baseline_se
    ),
    fill = "darkgoldenrod1") +
    stat_smooth(method = "glm",
                formula = y ~ ns(x, length(polar_directions[[i]])),
                linewidth = 0.3, color = "forestgreen") +
    geom_point(color = "#333132") +
    geom_label(aes(label = round(si, 2) , x = 315, y = cbss_max_y * 1.2),
               size = 3) +
    geom_vline(aes(xintercept = vector_sum), colour = "grey30",
               size = 0.75) +
    coord_polar(direction = 1, start = pi/2) +
    scale_x_continuous(
      breaks = c(0, 90, 180, 270),
      expand = c(0, 0),
      limits = c(0, 360)
    ) +
    scale_y_continuous(
      #trans = "sqrt",
      limits = c(0, cbss_max_y * 1.2)
    ) +
    facet_grid(cols = vars(Speed)) +
    ggtitle("1500-3000 ms (steady state) motion") +
    ylab("Spike rate (spikes/sec)") +
    theme_minimal()
}

## `summarise()` has grouped output by 'Speed', 'Direction'. You can override
## using the `.groups` argument.

bin10_polar_cbss[[1]]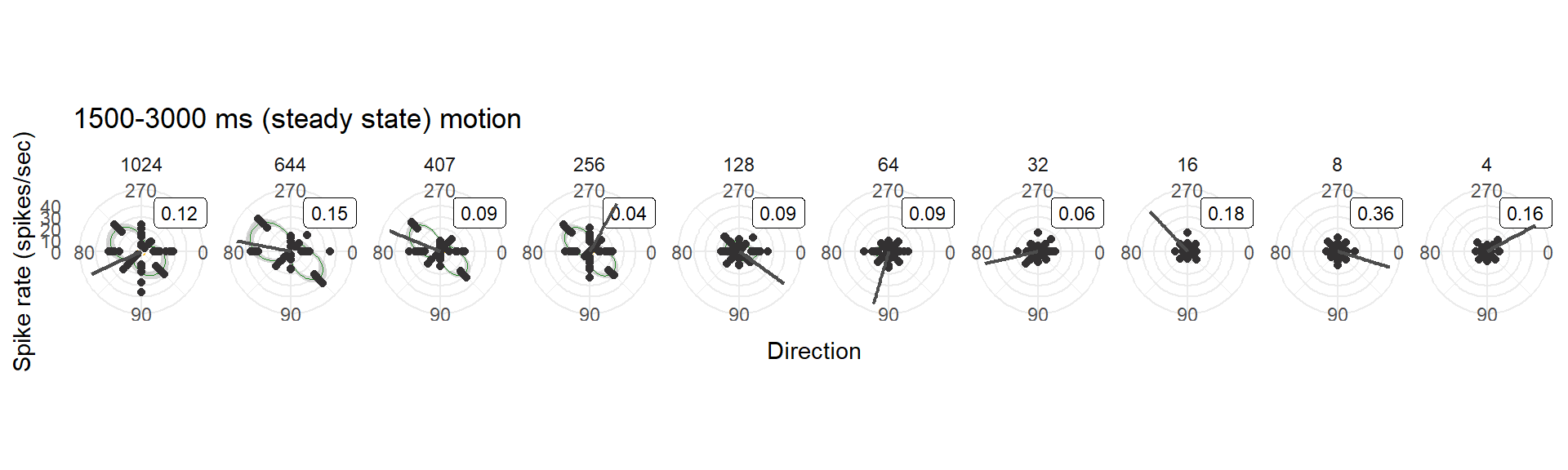

7.5 Using 0-500 ms (arbitrary epoch length)

## global baseline values, 0-500 msec motion period
bin10_polar_arb <- NULL
for (i in 1:length(bin10_filelist)) {
  arb_df <-
    bin10_data[[i]] %>%
    filter(Time_stand >= Static_end + 0.001) %>%
    filter(Time_stand <= Static_end + 0.500) %>%
    group_by(Speed, Direction, Replicate) %>%
    summarize(
      mean_spike_rate = mean(Spike_rate)
    )
  arb_360 <-
    arb_df %>%
    filter(Direction == 0) %>%
    transmute(
      Speed = Speed,
      Direction = 360,
      Replicate = Replicate,
      mean_spike_rate = mean_spike_rate)
  arb_vecsum_df <-
    arb_df %>%
    ungroup() %>%
    drop_na(mean_spike_rate) %>%
    group_split(Speed) %>%
    map(group_by, Direction) %>%
    map(summarize,
        mean_spike_rate = mean(mean_spike_rate) - unique(baseline_summary_df[[i]]$global_baseline),
        Speed = first(Speed)) %>%
    map(mutate,
        mean_spike_rate =
          case_when(min(mean_spike_rate) < 0 ~ mean_spike_rate + abs(min(mean_spike_rate)),
                    TRUE ~ mean_spike_rate)) %>%
    map(transmute,
        x = cos(Direction * pi / 180) * mean_spike_rate,
        y = sin(Direction * pi / 180) * mean_spike_rate,
        Speed = first(Speed)
    ) %>%
    map(summarise,
        x = mean(x),
        y = mean(y),
        Speed = first(Speed)) %>%
    map(transmute,
        vector_sum = (atan2(y, x) * 180 / pi) %% 360,
        Speed = first(Speed)
    ) %>%
    bind_rows()
  arb_si_df <-
    arb_df %>%
    ungroup() %>%
    drop_na(mean_spike_rate) %>%
    group_split(Speed) %>%
    map(group_by, Direction) %>%
    map(summarize,
        mean_spike_rate = mean(mean_spike_rate) - unique(baseline_summary_df[[i]]$global_baseline),
        Speed = first(Speed)) %>%
    map(mutate,
        mean_spike_rate =
          case_when(min(mean_spike_rate) < 0 ~ mean_spike_rate + abs(min(mean_spike_rate)),
                    TRUE ~ mean_spike_rate)) %>%
    map(transmute,
        a = (sin(Direction * pi / 180) * mean_spike_rate),
        b = (cos(Direction * pi / 180) * mean_spike_rate),
        c = mean(mean_spike_rate),
        Speed = first(Speed)
    ) %>%
    map(summarise,
        a = mean(a),
        b = mean(b),
        c = mean(c),
        Speed = first(Speed)) %>%
    map(transmute,
        si = sqrt(a ^ 2 + b ^ 2) / c,
        Speed = first(Speed)
    ) %>%
    bind_rows()

  arb_data <-
    arb_df %>%
    bind_rows(arb_360) %>%
    left_join(arb_vecsum_df, by = "Speed") %>%
    left_join(arb_si_df, by = "Speed") %>%
    drop_na(mean_spike_rate)
  arb_max_y <- max(arb_data$mean_spike_rate)

  bin10_polar_arb[[i]] <-
    arb_data %>%
    left_join(baseline_summary_df[[i]], by = "Speed") %>%
    ggplot(aes(x = Direction, y = mean_spike_rate)) +
    geom_ribbon(aes(
      x = Direction,
      ymin = global_baseline - global_baseline_se,
      ymax = global_baseline + global_baseline_se
    ),
    fill = "darkgoldenrod1") +
    stat_smooth(method = "glm",
                formula = y ~ ns(x, length(polar_directions[[i]])),
                linewidth = 0.3, color = "forestgreen") +
    geom_point(color = "#333132") +
    geom_label(aes(label = round(si, 2) , x = 315, y = arb_max_y * 1.2),
               size = 3) +
    geom_vline(aes(xintercept = vector_sum), colour = "grey30",
               size = 0.75) +
    coord_polar(direction = 1, start = pi/2) +
    scale_x_continuous(
      breaks = c(0, 90, 180, 270),
      expand = c(0, 0),
      limits = c(0, 360)
    ) +
    scale_y_continuous(
      #trans = "sqrt",
      limits = c(0, arb_max_y * 1.2)
    ) +
    facet_grid(cols = vars(Speed)) +
    ylab("Spike rate (spikes/sec)") +
    ggtitle("0-500 msec motion") +
    theme_minimal()
}

## `summarise()` has grouped output by 'Speed', 'Direction'. You can override
## using the `.groups` argument.

bin10_polar_arb[[1]] 

## Warning: Removed 17 rows containing missing values (`geom_smooth()`).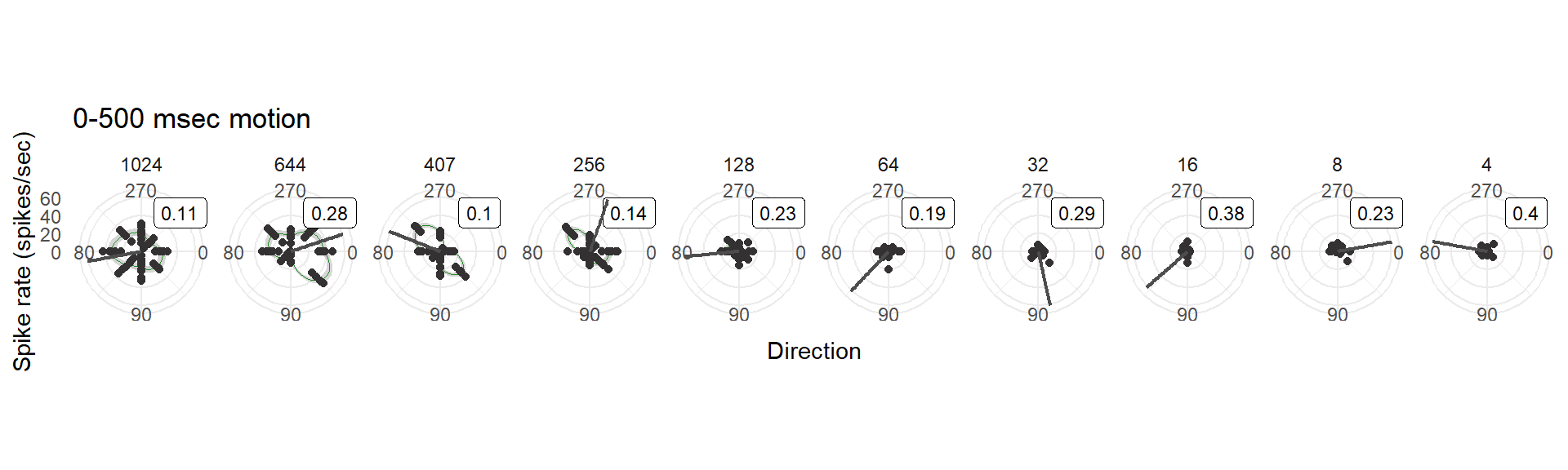

7.6 Construct a multi-panel plot

We can use the handy cowplot package to construct a multi-panel plot.

cow_polar <- NULL
for (i in 1:length(bin10_basenames)) {
  cow_polar[[i]] <-
    plot_grid(bin10_polar_naive[[i]],
              bin10_polar_cbit[[i]],
              bin10_polar_cbss[[i]],
              bin10_polar_arb[[i]],
              ncol = 1)
}

## Warning: Removed 149 rows containing missing values (`geom_smooth()`).

## Warning: Removed 17 rows containing missing values (`geom_smooth()`).

cow_polar[[1]]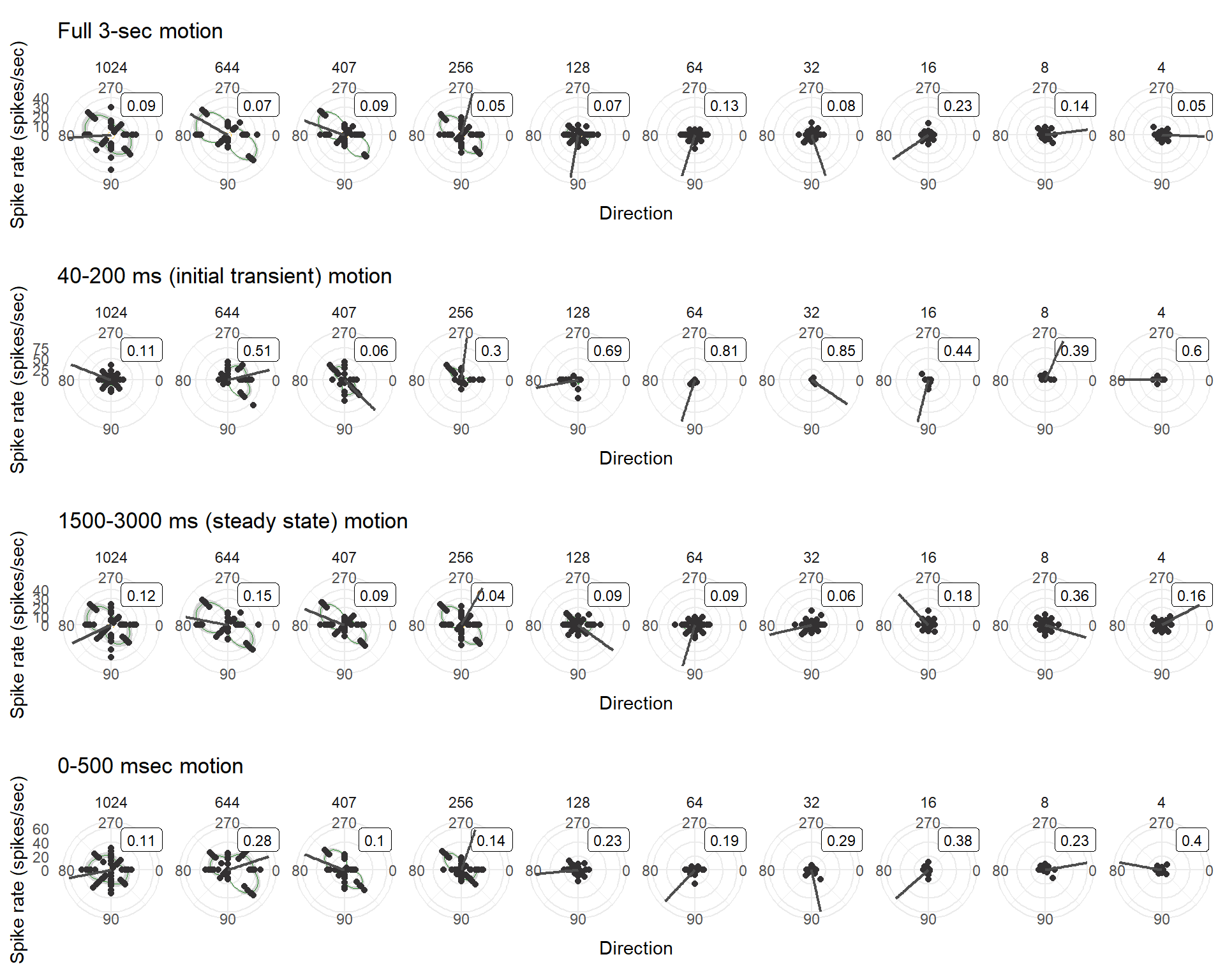

This plot can also be written directly to PDF.

for (i in 1:length(cow_polar)) {
  pdf(file =
        paste0("./plot_pdfs/",
               bin10_basenames[i],
               "_polar_set.pdf"),
      width = 22, height = 12,
      pagecentre = TRUE, colormodel = "srgb")
  plot(cow_polar[[i]])
  dev.off()
}